 E’ con piacere che rilancio la chiamata che l’amica Annarita Ruberto fa per il 69° Carnevale della Matematica a cui parteciperò con una mia esperienza didattica.
E’ con piacere che rilancio la chiamata che l’amica Annarita Ruberto fa per il 69° Carnevale della Matematica a cui parteciperò con una mia esperienza didattica.
Nel mio caso, come sempre, uso questo evento per mettere a fuco idee didattiche, rivedere esperienze passate, riflettere su strategie nuove e su come cambiare, è un momento di didattica “open” un momento di apprendimento collettivo dove le esperienze dei molti diventano un concentrato di sana e appassionata didattica.
La pubblicazione degli articoli sarà il 14 gennaio 2014 ed avrà per tema “Macchine matematiche antiche e moderne“, un argomento interessantissimo. Come sempre però, se l’argomento non è di vostro gradimento potrete sempre dare il vostro contributo con altri temi, purché si parli di Matematica va sempre bene!
Al carnevale possono partecipare tutti: studenti, insegnanti, appassionati di matematica.
Dal blog di Annarita
…
Il tema, in ogni caso, è davvero vasto e dovreste trovare facilmente qualcosa che fa al caso vostro. Potreste parlare di pantografi, parabolografi, iperbolografi, ellissografi, sistemi articolati e biellismi di vario genere in relazione ai vari tipi di trasformazioni geometriche che consentono di eseguire. E cosa dire delle coniche, considerate sia come luoghi di punti, sia come inviluppi? Su questo terreno, potreste pensare ai diversi metodi per la loro generazione (angoli in movimento, fili tesi congiungenti punti omologhi su rette corrispondenti, ecc.) in un excursus storico, ripercorrendo le orme degli antichi geometri greci.E non dimenticate le macchine per eseguire calcoli: dall’abaco, alla pascalina e alle moderne calcolatrici. Pensate che la tavola Pitagorica, all’origine, non era una tavola di moltiplicazione, come noi oggi la consideriamo, bensì un abaco attribuito ai neopitagorici, la cui struttura suggeriva chiaramente l’idea della notazione scritta posizionale dei numeri.
L’esplorazione può continuare con i software di geometria dinamica quali:
– GeoGebra e Cabri, vere macchine matematiche virtuali;
– Maxima, software di tipo CAS (Computer Algebra System) Open Source per eseguire calcoli algebrici e simbolici;
– Scilab, pacchetto di programmi gratuiti per la computazione numerica sviluppati dallo INRIA e dallo ENPC in Francia, simile a Matlab.
…
Il termine per la presentazione dei prori interventi è il 12 gennaio 2014.
Per maggiori informazioni sull’evento e sulla modalità di partecipazione, vi invito a consultare Matem@ticaMente.
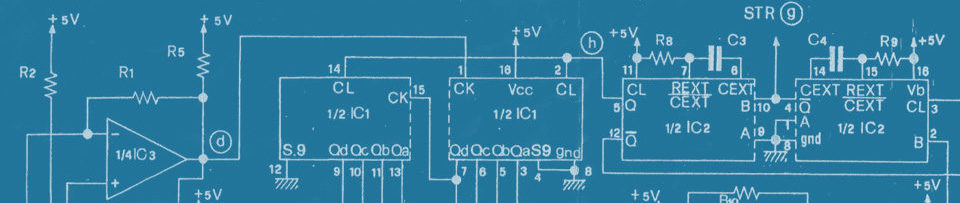

 Gli studente che seguono corsi di elettronica e sistemi sanno che è essenziale conoscere il sistema binario e come conseguenza calcolare velocemente le potenze di 2 di un numero. Come più volte spiegato a lezione riassumo di seguito il metodo, che con un po’ di allenamento vi renderà velocissimi nel calcolo mentale.
Gli studente che seguono corsi di elettronica e sistemi sanno che è essenziale conoscere il sistema binario e come conseguenza calcolare velocemente le potenze di 2 di un numero. Come più volte spiegato a lezione riassumo di seguito il metodo, che con un po’ di allenamento vi renderà velocissimi nel calcolo mentale.